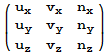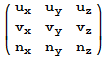3D Computer Graphics, Rotations, and Lazy Professors

| World Coordinates and the Viewing-Reference Coordinates | |
|---|---|
|
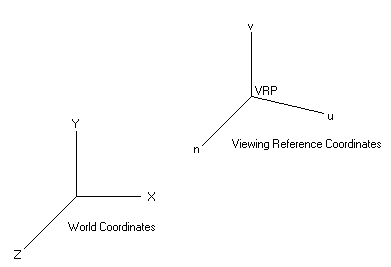
The situation is we have two coordinate systems, shown below. (To fix ideas, we are thinking of the
coordinates as elements of R3, not R4 as a projective space.
Then standard linear algebra applies.)
The world coordinate system is how our objects
are originally specified in 3 dimensions. The viewing-reference coordinate system's claim to fame is that it
contains the uv-plane, which
is the viewing plane (or projection plane). The viewing plane is of course 2 dimensional, and
ultimately part of it will be used to represent the 2D computer screen on which the user will see the original
3D world rendered. The viewing plane is defined by specifying a point on the
plane, the view reference
point (VRP), and a direction which will be taken as normal to the viewing plane, which in the diagram is
indicated by the direction along the n-axis.
The v-axis specifys the up direction, and is orthogonal to n. Once the n and v
directions are known, then the u-axis is defined so that u,v, and n form a
right-handed coordinate system.
So, we will be working in the viewing reference coordinate system and thus we have to perform the
following operations:
The translation indicated in step 1 is routine, and the result is shown below:
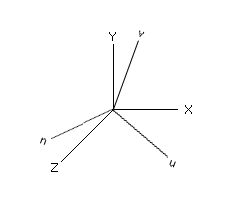
Step 2 is what concerns us and is where Foley can be improved on. Our task is to figure out how
to rotate the the view coordinate system into the world coordinate system.
To define a linear transformation (and a rotation is a linear transformation)
it is sufficient to specify its action on any basis. So,
Let {i,j,k} be the standard ordered basis of R3. Let {u,v,n} be unit vectors along the u,v, and n axes. They also are a basis of R3. Then the rotation T: R3 → R3 is defined by
u |→ i,
The first thing to note is we are done. That's it. T is completely specified.
Given any vector α ∈ R3, we can expand it as
α = a u + b v + c n ,
and the rotation acting on α is then
T(α) = T(a u + b v + c n)
The matrix A of a linear transformaion T:Rn → Rn relative to an ordered basis
β = {β1,β2,...,βn} is defined by
T(βj) = Σ Aij βi (j=1,2,..,n)
Notice that the matrix of the transformation is defined by specifying the
action of the transformation on a basis, and as I have already indicated, we
have been given that in the problem statement. Incidentally
this is the standard method, and it is not the method Foley uses. Foley's
method will work to determine the matrix with respect to an
orthonormal basis, but it does not work for an arbitrary basis. If you
can guarantee your students are only going to work with rotations in R3,
and only with orthonormal bases, and not arbitrary linear transformations and bases, then perhaps
Foley might be OK, but that is quite an assumption. Better to learn how to do it in
the general case.
So, let's make the construction of the matrix A explicit:
T-1(i) = uxi + uyj + uzk
and so the matrix of T-1 (not T, but the inverse of T) relative to the standard
basis is given by:
Again, that is the matrix of T-1, not T. But we want the matrix of T.
To get that, we finally use the fact that rotations are othogonal transformations, which, by
definition means that TTt= I, where Tt is the transpose of T.
Thus,
Tt = T-1 and so,
T= (T-1)t
Finally, taking the transpose of the matrix above for T-1
, we get the desired matrix for T:
and that is the result Foley gets for the rotation matrix relative to the
standard basis of R3.
|