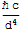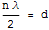The Casimir Effect

IF you take a charged parallel plate capacitor and increase the distance between its plates, you will find that you have to have to do work to overcome the attractive Coulomb force between the plates. If the capacitor plates have area A, and a surface charge density sigma, the amount of work you have to do to increase the plate separation by an amount delta d is:
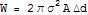
If the capacitor is uncharged, you would expect that no work is required to increase the plate separation (you may assume the ideal case of massless, perfectly conducting plates). However, in 1948, Hendrik Casimir realized, amazingly enough, that is not true.
Casimir showed that an attractive (non-gravitational) quantum force exists between two uncharged perfectly conducting parallel plates, and this result is called the Casimir Effect. For a plate separation of d, the Casimir force per unit area is given by:
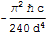
The exact derivation of the Casimir force equation above is a little involved, but
a heuristic argument, plus or minus a multiplicative constant,
is possible via dimensional analysis.The first step in any dimensional analysis argument is
to specify on what physical quantities the object in question should depend. As
the Casimir force is a quantum effect, it must depend on Planck's constant h.
It should also depend on d, the plate separation. If the force is mediated by particles
that travel at c (as is the case of the electromagnetic force and photons), then
it should also depend on c.So we want Force/area = F(h,d,c) as the required functional dependence, the exact
form of which we must determine.
The only combination of h [J T], d [L] and c [L/T2] that has units of
Force/area is: